Simple and Complex Contagion

In today's hyper-connected world, understanding contagion dynamics goes beyond epidemiology, extending into social behaviour, information dissemination, and political mobilisation. At its core, contagion theory seeks to explain how things spread. There are two primary types of contagion: simple contagion, which involves spreading information or diseases through single exposures based on a certain probability, and complex contagion, where multiple affirmations from trusted sources are required for transmission. This distinction is crucial in understanding health-related outbreaks and spreading ideas, behaviours, and innovations across networks.

Simple contagion

• Mechanism: Simple contagion refers to the process where exposure to an infected node (or piece of information) once is sufficient for transmission. Examples include the spread of a virus, rumors, or job information. This model is predicated on the assumption that each contact has a probability (ß) of passing the contagion.

  ß

• Diffusion Process: Individuals in a network can be in two states: activated (infected) or inactivated (susceptible). The transition from susceptible to infected depends on the probability of contact with an infected individual.

The Role of Ties

• Weak Ties: Described as connections with distant friends, neighbors, or colleagues, weak ties are less emotionally intense and involve less frequent interaction. However, they're crucial for spreading simple contagions because they act as bridges between different social circles, providing access to new information and opportunities. Mark Granovetter's research highlighted how people often find jobs through acquaintances rather than close friends, underscoring the "strength of weak ties."
• Strong Ties: These are connections with family, partners, or close friends—your core discussion network. While they offer emotional support and frequent contact, they tend to be part of a closed network where information circulates within the same group, leading to redundancy.

Mechanism of complex contagion

• Complex Contagion: Contrasts with simple contagion by requiring multiple exposures or endorsements from trusted sources before adoption occurs. This mechanism is typical for behaviors or ideas that are risky, costly, or deviate from established norms, such as adopting a new health behavior or participating in high-risk social movements.
• Strong Ties: These are connections with family, close friends, or core discussion networks where there's emotional intensity and frequent contact. Strong ties are essential for complex contagion because they provide the repeated, credible exposures necessary for transmission. The lecture cites examples where movements or behaviors spread through densely connected networks rather than sparse ones with weak ties, demonstrating the power of strong ties in complex contagion.

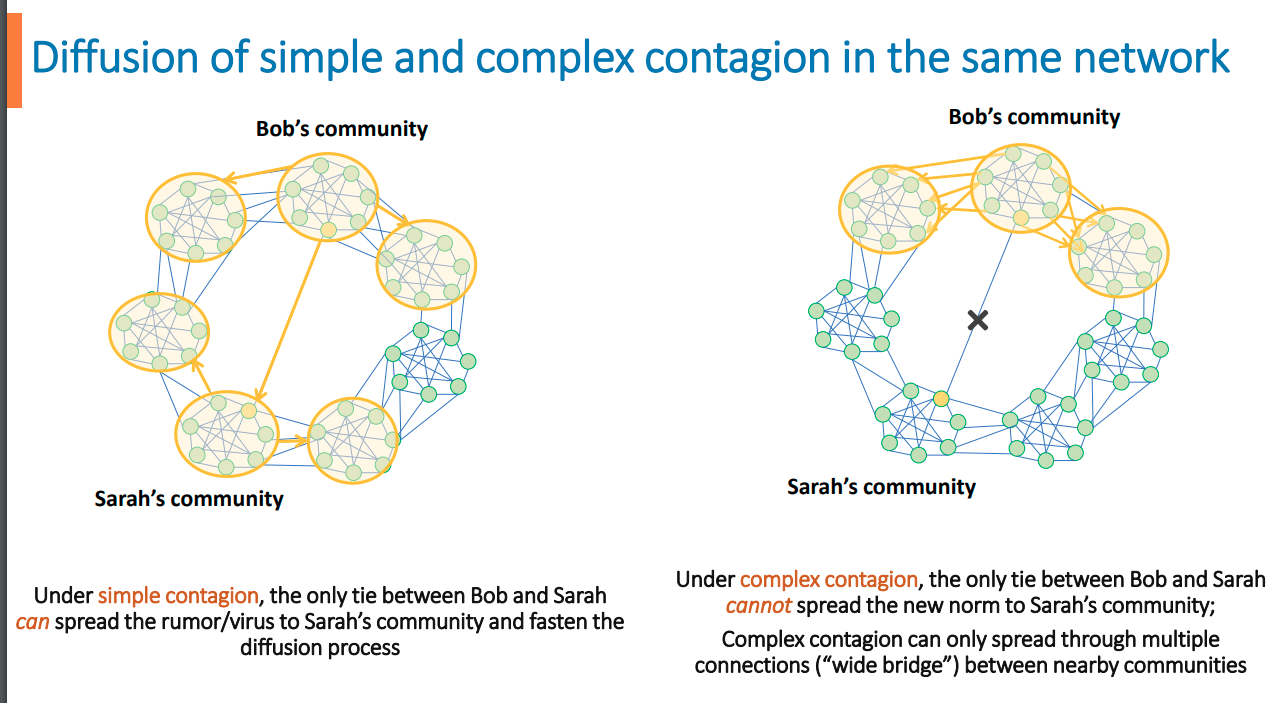
Width of a bridge decides the diffusion of

complex behavior

A crucial aspect of this theory is the importance of "wide bridges" in the diffusion of complex contagions. A bridge in a network connects two distinct communities or clusters. The width of a bridge is determined by the number of overlapping ties it comprises, not just its length. In the context of social networks:

• Wide Bridges: These are connections between communities that involve numerous overlapping ties. Wide bridges are essential for the spread of complex contagions because they ensure multiple exposures to the new idea or behavior from various sources, thereby increasing the likelihood of adoption within each connected community.
• Weakness of Long Ties: Contrary to Granovetter's "strength of weak ties" which emphasizes the role of weak, long ties in spreading information across a network, Centola and Macy suggest that for complex contagions, mere length or weakness of ties isn't sufficient. Long ties that do not have the redundancy (or width) required to reinforce the credibility or desirability of the new norm or behavior are less effective in spreading complex contagions.

Spatial Diffusion of Social Movements

The study also touches upon why social movements tend to spread spatially, attributing this pattern to the natural occurrence of wide bridges in spatial networks. In physical communities or regions, overlapping social ties are common, making it easier for complex behaviors to permeate through these wide bridges, enhancing the spatial diffusion of movements or behaviors.

Models in network theory

Independent Cascade Model

The Independent Cascade Model is a fundamental framework for understanding how actions, information, or influence spreads from one node to another within a network. It's particularly useful in modeling how individuals adopt new behaviors or information based on interactions with their peers. Here’s how it works:

• Nodes can have two states — active (S=1) and inactive states (S=0); once activated, can not be inactive again (e.g., Bob used the product)

• Initially, a select number of nodes (seed nodes) are activated.

• These activated nodes then have a single chance to activate their neighboring nodes based on a predetermined probability.

• The process continues until no further activations can occur, either because all nodes have been activated or because the probability of further activations drops to zero.

  

SIR Model and Its Variants

The SIR Model is a classic model from epidemiology, representing the spread of contagious diseases. It categorizes the population into three compartments:

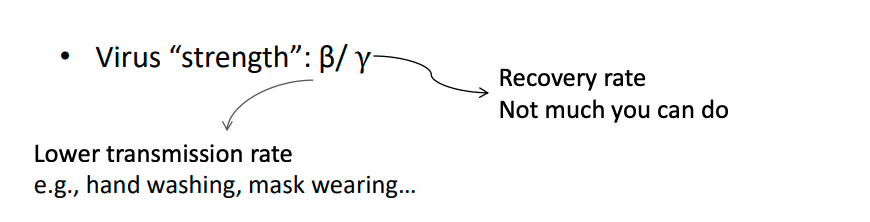
• Susceptible (S): healthy people that can catch the virus with the contact of infected people, with certain probability 𝛽;
• Infected (I): people who have been infected and are capable of infecting susceptible individuals. (being infectious within 1/ γ time steps)
• Recovered (R): people who have been infected and have either recovered from the disease and entered the removed compartment, or died.

The SIR model, and its variants like the SEIR model (which adds an Exposed (E) category for those infected but not yet infectious), provide insights into disease dynamics, helping to predict the course of an outbreak and evaluate intervention strategies.

Threshold Model

The Threshold Model explains the adoption of behaviors or norms within a society, where each individual has a specific threshold for adopting a new behavior. This threshold can be influenced by several factors, including the proportion of peers who have already adopted the behavior. In this model:

• Behavior change occurs when the cumulative influence from a person’s network exceeds their threshold.
• The model highlights the importance of social reinforcement, especially for behaviors that require a higher degree of social validation before adoption.

Linear Threshold Model

Key Components of the Model

• Node States: Each node (representing an individual or entity in the network) can be in one of two states: active (𝑆𝑖 = 1) or inactive (𝑆𝑖 = 0). Once a node becomes active, it remains in that state permanently.
• Direct Neighbors and Influence: Every node has a set of direct neighbors, each exerting some influence on the node. This influence is quantified by weights (𝑤𝑗𝑖), where the sum of all influences from neighbors to a node is less than or equal to 1.
• Fractional Threshold (𝜃𝑖): Each node has a threshold that determines its susceptibility to activation. This threshold represents the minimum proportion of active neighbors required to activate the node, ranging between 0 (always activates) and 1 (never activates without full neighbor activation).

Activation Process

1. Review Neighbors' States: At each timestep, inactive nodes assess their direct neighbors.

2. Calculate Weighted Influence: For a given node, multiply each neighbor's state (active = 1, inactive = 0) by the influence weight from that neighbor to the node, summing these products.

3. Compare with Threshold: If the sum of the weighted influences exceeds the node's threshold, the node becomes active. Otherwise, it remains inactive.

   

Key Takeaways:

• Simple Contagion and Weak Ties: Simple contagions, like information spread or low-stakes behaviors, can efficiently propagate through weak ties, which connect disparate parts of a network.
• Complex Contagion and Strong Ties: Complex contagions, which involve behaviors that are costly, risky, or require significant lifestyle changes, rely on strong ties for propagation. These behaviors often require multiple exposures or social reinforcement from close contacts to overcome inherent barriers to adoption.
• Diffusion Models Provide Frameworks: These models offer theoretical frameworks to analyze how different types of information, diseases, or behaviors spread within networks. Understanding these mechanisms can help in designing more effective intervention strategies for public health, marketing, and beyond.

Each model highlights the complex interplay between network structure, the type of contagion, and the social dynamics at play, emphasizing that the spread of anything through a network—be it a virus, a rumor, or a new technology—is influenced by the underlying patterns of connections between individuals.